|
3.47.
Для элементов двутаврового и таврового сечений с полкой в более
обжатой зоне (черт. 30) расчет прочности на действие предварительного
обжатия производится следующим образом:
если
соблюдается условие
Np£
Rb(p) b'f h'f-
Rs Asp-
Rs As + Rsc
A's (132)
(т.е.
граница сжатой зоны проходит в полке), расчет производится как при
отсутствии полки в более обжатой зоне в соответствии с п. 3.46 при b
= b'f ;
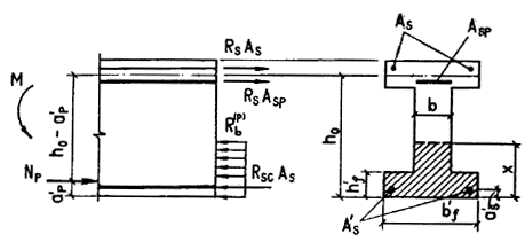
Черт. 30. Схема
усилий в поперечном сечении внецентренно обжатого железобетонного
элемента с полкой в сжатой зоне
если
условие (132) не соблюдается (т.е. граница сжатой зоны проходит в
ребре), расчет производится в зависимости от высоты сжатой зоны
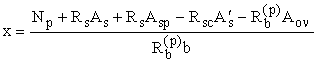 ,
,
а)
при
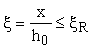 [см. формулу (21) п. 3.6 при
ssc,u
= 330
МПа] - из условия
[см. формулу (21) п. 3.6 при
ssc,u
= 330
МПа] - из условия
Npe £
Rb(p) bx (h0-
0,5x) + Rb(p) Aon
(h0-
0,5h¢f) +
Rsc A's (h0-
a¢s),
(133)
где
e - см. п. 3.48;
б)
при x
> xR
- из условия
Npe £
aR Rb(p)
bh02 + Rb(p)
Aon (h0- 0,5h¢f)
+ Rsc A's (h0- a¢s),
(134)
где
aR
= (1 -
0,5xR);
Aon=
(b¢f-
b)h¢f
— площадь сечения сжатых свесов.
Значения
xR
и aR
при ненапрягаемой арматуре менее обжатой зоны классов А-III и Вр-I
можно определять по табл. 33.
Если
x
> xR
, расчетную несущую способность на действие обжатия при необходимости
можно несколько увеличить, используя условие (133) при значении х,
определенном по формулам (130) или (131), в которых сила
Np уменьшается на величину Rb(p)
Аon.
3.48.
Значение е в условиях. (128), (129), (133) и (134) определяется по
формулам:
при
натяжении на упоры
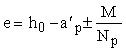 ; (135)
; (135)
при
натяжении на бетон
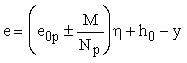 . (136) . (136)
В
формулах (135) и (136):
М — момент
от нагрузок, действующих в стадии изготовления; знак «плюс»
принимается, если момент усилия Np
относительно арматуры S и момент М
совпадают по направлению, знак «минус» — если
направления этих моментов противоположны;
t0p
— эксцентриситет силы Np относительно центра тяжести
приведенного сечения;
h
— см. пп. 3.39 и 3.45;
у —
расстояние от центра тяжести приведенного сечения до наиболее обжатой
грани.
Значение
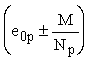 в формуле (136) принимается не менее ea
(см. п. 3.35).
в формуле (136) принимается не менее ea
(см. п. 3.35).
Примеры расчета
Пример
20. Дано: ребристая плита покрытия длиной 12 м
с поперечным сечением ребра по черт. 31; напрягаемая арматура
из канатов класса К-7 натягивается на упоры; предварительное
напряжение с учетом первых потерь при
gsp
> l ssp1
= 900 МПа;
передаточная прочность тяжелого бетона Rbp
= 25 МПа; масса плиты 7,4 т; монтажные петли расположены на
расстоянии 800 мм от торца плиты.
Требуется
проверить прочность плиты в стадии изготовления.
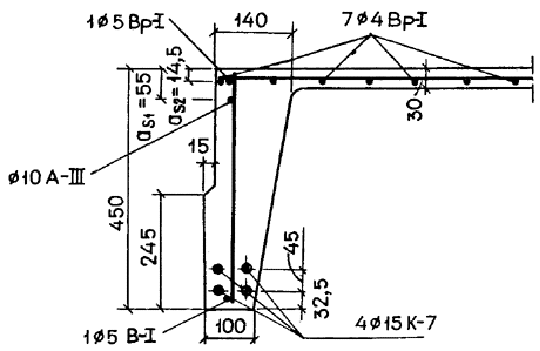
Черт. 31. К
примеру расчета 20
Р
а с ч е т. Из черт. 31 видно, что в наиболее обжатой зоне
располагается напрягаемая арматура класса К-7, площадью А¢sp
= 566 мм2 (4 Æ
15). Heнапрягаемую арматуру 1 Æ
5 класса Вр-I, расположенную в этой зоне, в
расчете не учитываем, поскольку она не удовлетворяет конструктивным
требованиям п. 5.39.
В
менее обжатой зоне располагается ненапрягаемая арматура с физическим
пределом текучести 1 Æ
10 классов А-III (Аs1 = 78,5
мм2) и 1 Æ
5 Вр-I +7 Æ
4 Вр-I (Аs2 = 19,6
+ 87,9 = 107,6
мм2).
Поскольку
значения Rs для арматуры классов
А-III и Вр-I (Æ4
и Æ5)
близки, принимаем точку приложения равнодействующей усилий в арматуре
менее обжатой зоны в центре тяжести сечения этой арматуры, и тогда
расстояние ее от верхней грани сечения равно:
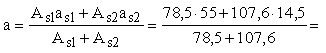 31,6
мм . 31,6
мм .
Следовательно,
h0 = h
-
а = 450 -
31,6 = 418 мм.
Из
черт. 31 имеем
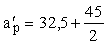 = 55.
= 55.
Расчетное
усилие обжатия, согласно п. 3.44, равно:
Np
= (ssp1-
330)А'sp = (900
-
330) 566 = 322 600 Н = 322,6 кН.
Определяем
значение е согласно п. 3.48. Равномерно распределенная нагрузка от
собственного веса плиты, учитывая указания п. 2.14 и коэффициент
надежности по нагрузке gf
= 1,1, будет
равна:
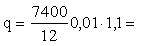 6,8
кН/м. 6,8
кН/м.
Поскольку
монтажные петли располагаются на расстоянии l = 0,8 м от торца,
невыгоднейший момент от собственного веса, растягивающий верхнюю
грань, будет возникать при подъеме плиты. Определим этот момент с
учетом коэффициента 1,4 (см. п. 1.9) для половины сечения плиты:
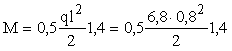 = 1,52 кН×м. = 1,52 кН×м.
Тогда
e = h0-
a¢p
+
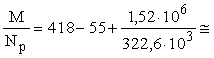 368
мм. 368
мм.
Расчетное
сопротивление бетона, соответствующее передаточной прочности
Rbp = 25 МПа согласно
табл. 13 при gb2
= 1, равно Rb(p)
= 14,5 МПа, а с учетом коэффициента gs8
= 1,1 (см. табл. 14, поз. 5) - Rb(p)
= 1,1×14,5
= 16 МПа.
Поскольку
ширина ребра b переменна, принимаем в первом приближении ширину ребра
посередине высоты сжатой зоны равной xRh0.
Из табл. 33 при Rbp = 25 МПа,
тяжелом бетоне и проволочной напрягаемой арматуре находим xR
= 0,52. Тогда
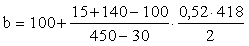 = 114,2 мм .
= 114,2 мм .
Высота
сжатой зоны при Аsp = 0 и А's
= 0 равна:
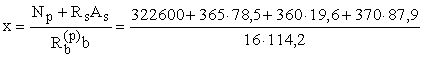 =
214,2 мм. =
214,2 мм.
Поскольку
x
= x/h0 = 214,2
/ 418 = 0,512 <
xR
= 0,52, прочность проверяем из условия (128). При этом ширину ребра
не пересчитываем, так как полученное значение x
близко к xR:
Rb(p)
bx (h0-
0,5х) = 16 ×
114,2 ×
214,2 (418 -
0,5 ×
214,2) =
= 121,7 ×
106 Н×мм
= 121,7 кН×м
> Np e = 322,6 ×
0,368 = 118,7 кН×м,
т.е.
прочность в стадии изготовления обеспечена.
Центрально-растянутые элементы
3.49
(3.26). При расчете сечений центрально-растянутых железобетонных
элементов должно соблюдаться условие
N
£
h
Rs Asp,tot + Rs As,tot ,
(137)
где
h
— см. п. 3.7;
Asp,tot,
As,tot — площади сечения всей продольной
соответственно напрягаемой и ненапрягаемой арматуры.
Внецентренно растянутые элементы
РАСЧЕТ ЭЛЕМЕНТОВ
ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ
ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ
3.50
(3.27). Расчет прямоугольных сечений внецентренно растянутых
элементов с арматурой, сосредоточенной у наиболее растянутой и у
сжатой (наименее растянутой) граней, должен производиться в
зависимости от положения продольной силы N:
а)
если продольная сила N приложена между
равнодействующими усилий в арматуре S и
S' (черт. 32, а), т.е. при е' £
h0 — а¢,
- из условий:
Ne'
£
(hRsAsp
+ RsAs) (h0-
а¢);
(138)
Ne
£
(hRsA¢sp
+ RsA¢s)
(h0
-
а¢)
, (139)
где
h
—см. п. 3.7;
при
симметричной арматуре используется только условие (138);
б)
если продольная сила N приложена за пределами расстояния между
равнодействующими усилий в арматуре S и S' (черт. 32,
б), т.е. при е' > h0-
а¢,
- из условия
Ne
£
Rb bx(h0-
0,5x) +
Rsc A's (h0-
а¢s)
+ ssc
A¢sp
(h0-
a¢p
) , (140)
при
этом высота сжатой зоны х определяется по формуле
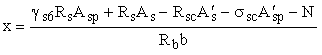 , (141) , (141)
где gs6
- см. формулу (23); при этом
 допускается определять из формулы (141) без учета gs6;
допускается определять из формулы (141) без учета gs6;
ssc
— см. п. 3.8.
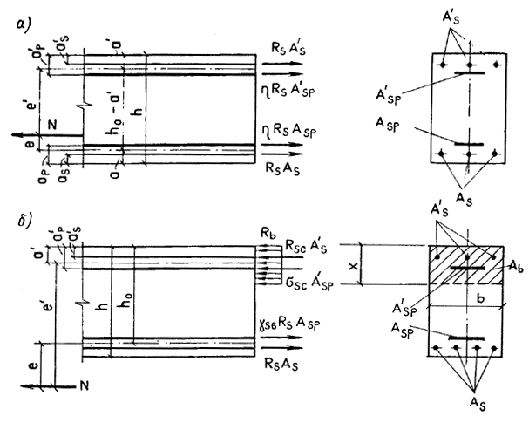
Черт. 32. Схема
усилий в прямоугольном сечении внецентренно
растянутого
железобетонного элемента при расчете его на прочность
а —
продольная сила N приложена между равнодействующими усилий
в
арматуре S и S'; б — то же, за
пределами расстояния между
равнодействующими усилий в арматуре S
и S'
Если
полученное из расчета по формуле (141) значение х >
xRh0,
в условие (140) подставляется х = xRh0,
где определяется согласно п. 3.6.
Если
х < 0, прочность сечения проверяется из условия (138).
При
применении ненапрягаемой арматуры с условным пределом текучести
следует учитывать примечание к п. 3.3.
П
р и м
е ч а
н и е.
Если при е' > h0-
а' высота сжатой зоны, определенная без учета ненапрягаемой арматуры
S',
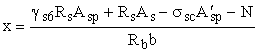
меньше
2a¢s,
расчетную несущую способность можно несколько увеличить, произведя
расчет по формулам (140) и (141) без учета ненапрягаемой арматуры S'.
3.51.
Элементы прямоугольного сечения с симметричной арматурой,
расположенной в несколько рядов по высоте сечения, рассчитываются при
силе N, приложенной между крайними рядами арматуры, из условия
Ne1£
h
Rs Ssp + Rs Ss ,
(142)
где
e1 — расстояние от силы N до оси,
перпендикулярной направлению эксцентриситета и проходящей через
наименее растянутый ряд арматуры;
Ssp,
Ss — статические моменты площади
сечения соответственно всей напрягаемой и всей ненапрягаемой арматуры
относительно той же оси;
h
— см. п. 3.7.
Если
сила N приложена за пределами расстояния между крайними рядами
арматуры, расчет производится по формулам общего случая согласно п.
3.53.
3.52.
Определение требуемого количества продольной арматуры производится
следующим образом:
а)
при e' £
h0-
а' площадь сечения напрягаемой арматуры S и S¢
определяется соответственно по формулам:
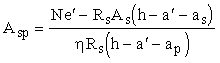 ; (143) ; (143)
 ; (144) ; (144)
б)
при e' > h0-
а' площадь сечения напрягаемой арматуры S
определяется по формуле
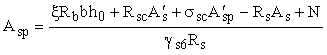 , (145)
, (145)
где
x
определяется по табл. 28 в зависимости от значения
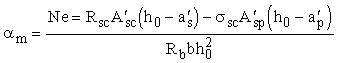 ; (146)
; (146)
gs6
— см. п. 3.7.
При
этом должно соблюдаться условие am£
aR
= xR
(1 -
xR/2)
(xR
— см. табл. 26 или 27). В противном случае следует увеличить
площадь сечения ненапрягаемой арматуры A's,
повысить класс бетона или увеличить размеры сечения.
Если
am
< 0, площадь сечения напрягаемой арматуры S
определяется по формуле (143).
При
подборе симметричной напрягаемой арматуры в первом приближении в
формулах (145) и (146) принимается A¢sp
= 0. При этом, если напряжение ssc
сжимающее (т.e. ssc
> 0), повторный расчет можно не производить.
П
р и м
е ч а
н и е. При
e' > h0-
a' и при отсутствии напрягаемой арматуры S' необходимое
количество напрягаемой арматуры S можно несколько снизить, если
значение x,
определенное по табл. 28 без учета ненапрягаемой арматуры S', т. e.
по значению
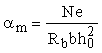 ,
оказывается меньше 2a's/h0.
В этом случае площадь сечения напрягаемой
арматуры S определяется по формуле ,
оказывается меньше 2a's/h0.
В этом случае площадь сечения напрягаемой
арматуры S определяется по формуле
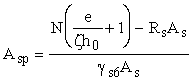 , (147)
, (147)
где
значение z
и значение x,
необходимое для вычисления gs6,
определяются по табл. 28 в зависимости от
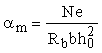 . .
Общий случай расчета нормальных сечений
внецентренно растянутого элемента
(при
любых сечениях, внешних усилиях и любом армировании)
3.53.
Расчет нормальных сечений внецентренно растянутого элемента в общем
случае (черт. 33) должен производиться из условия
Ne'
£
S
ssi
Ssi-
Rb Sb ,
(148)
где e' —
расстояние от продольной силы N до оси, параллельной прямой,
ограничивающей сжатую зону и проходящей через точку сжатой зоны,
наиболее удаленную от указанной прямой;
ssi
— напряжение в 1-м стержне продольной арматуры;
Ssi
— статический момент площади сечения i-го стержня продольной
арматуры относительно указанной оси;
Sb
— статический момент площади сечения сжатой зоны бетона
относительно указанной оси.

Черт. 33. Общий
случай расчета внецентренно растянутого элемента
I
— т | 