Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен их шаг.

Р а с ч е т. Наибольшая поперечная сила в опорном сечении равна:

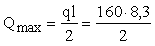= 664 кН ,

где q = n + g = 114 + 46 = 160 кН/м.

Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.23б.

Поскольку j_n = 0,1 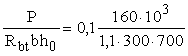= 0,693 > 0,5,

то принимаем „ = 0,5.

Из формулы (73) при j_f = 0 и j_b2 = 2 (см. табл. 29) получаем:

M_b = j_b2 (1 + j_n) R_bt b h₀² = 2×1,5×1,1×300×700 = 485•10 H×мм = 485 кН×м;

q₁ = g + n/2 = 46 + 114 / 2 = 103 кН/м (Н/мм);

Q_b1 = 2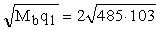 = 447 кН.

Так как 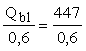= 745 кН > Q_max = 664 кН,

интенсивность хомутов определяется по формуле

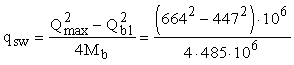= 124,3 Н/мм.

При этом 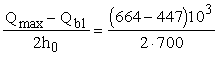= 155 > q_sw = 124,3 Н/мм,

следовательно, принимаем q_sw = 155 Н/мм.

Согласно п. 5.42, шаг у опоры должен быть не более 1/3h = 800/3 = 267 мм и не более 500 мм, а в пролете - не более 3/4h = 600 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

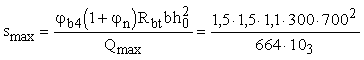= 548 мм.

Принимаем шаг хомутов у опоры s₁ = 250 мм, а в пролете - 2s₁ = 500мм.

Отсюда А_sw = q_sw s / R_sw = 155 • 250/290 = 134 мм².

Принимаем в поперечном сечении два хомута диаметром 10 мм (A_sw = 157 мм²).

Тогда 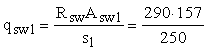= 182 Н/мм ;

q_sw2 = 0,5q_sw1 = 91 Н/мм.

Длину участка с наибольшей интенсивностью хомутов q_sw1 определяем согласно п. 3.24.

Так как q_sw1- q_sw2 = 182 - 91 = 91 Н/мм < q₁ = 103 Н/мм, значение с равно:

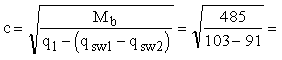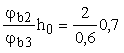6,36 м > = 2,33 м.

Принимаем с = 2,33 м.

По формуле (77) при q_sw = q_sw1 = 182 Н/м вычисляем c₀₁:

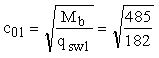= 1,632 м.

Тогда =

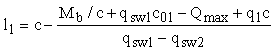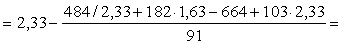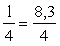1,45 м < = 2,08 м.

Принимаем длину участка с шагом хомутов s = 250 мм не менее 2,08 м.

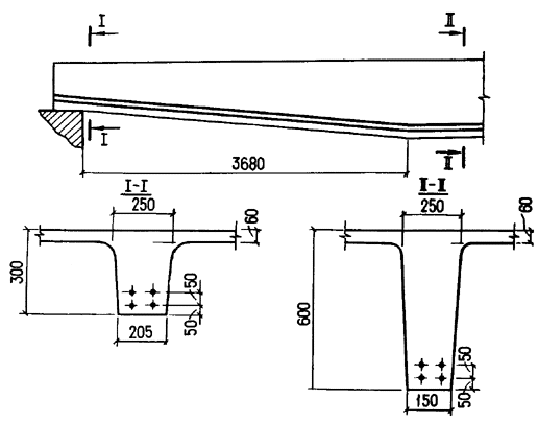
Пример 13. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт. 22, а; размеры поперечного сечения — по черт. 22, б; бетон тяжелый класса В50 (R_bt = 1,4 МПа при g_b2 = 0,9); хомуты из арматуры класса A-III (R_sw = 285 МПа); усилие предварительного обжатия Р = 640 кН.

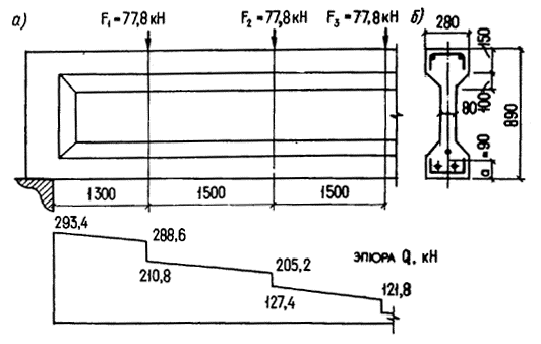
Черт. 22. К примеру расчета 13

Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен их шаг.

Р а с ч е т. Сначала определим, согласно п. 3.22, величину М_b:

j_b2 = 2 (см. табл. 29); h'_f = 150 + 100/2 = 200 мм (см. черт. 22,б);

b'_f- b = 280 - 80 = 200 мм < 3h¢_f; h₀ = 890 - 90 = 800 мм;

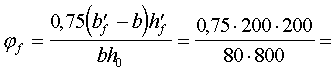0,469 < 0,5 ;

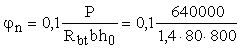= 0,714 > 0,5 .

Принимаем j_n = 0,5.

Поскольку 1 + j_f + j_n > 1,5, принимаем 1 + j_f + j_n = 1,5, M_b = j_b2 (1 + j_f + j_n) R_bt b h₀² = 2 × 1,5 × 1,4 × 80 × 800² = 215 × 10⁶ Н×мм = 215 кН×м.

Определим требуемую интенсивность хомутов согласно п. 3.23а, принимая длину проекции наклонного сечения с равной расстоянию от опоры до первого груза - с₁ = 1,3 м.

Поперечная сила на расстоянии c₁ от опоры равна Q₁ = 288,6 кН (см. черт. 22, a).

Из формулы (72) имеем

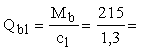164,5 кН > Q_b,min = j_b3 (1 + j_f + j_n) R_bt b h₀=
= 0,6 × 1,5 × 1,4 × 80 × 800 = 80,64 кН.

Тогда x₁ =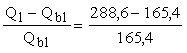 = 0,75.

Поскольку c₁ = 1,3 м < 2h₀ = 2 × 0,8 = 1,6 м, принимаем c₀ = c₁ = 1,3 м;

x₀₁ = 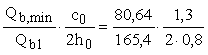= 0,396 .

Так как x₀₁ = 0,396 < x₁ = 0,75 < 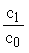= 1, значения q_sw(1) определяем по формуле (80):

q_sw(1) = 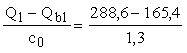= 94,8 кН/м.

Определим q_sw(2) при значении с, равном расстоянию от опоры до второго груза, с₂ = 2,8 м:

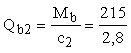= 76,8 кН < Q_b,min = 80,64 кН.

Принимаем Q_b2 = 80,64 кН.

Соответствующая поперечная сила равна Q₂ = 205,2 кН.

Поскольку c₂ = 2,8 м > 2h₀ = 1,6 м, принимаем c₀ = 2h₀ = 1,6 м;

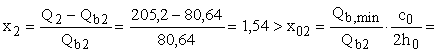
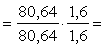1;

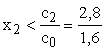= 1,75.

Следовательно, значение q_sw(2) определяем по формуле (80):

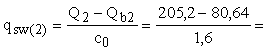77,85 кН/м.

Принимаем максимальное значение q_sw = q_sw(1) = 94,8 кН•м.

Согласно п. 5.42, шаг s₁ у опоры должен быть не более 1/3h = 890/3 = 297 мм и не более 500 мм, а в пролете — не более 3/4h = 3/4 • 890 = 667 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

s_mах = j_b4 (1+j_n) R_btbh₀² / Q_max = 1,5×1,5×1,4×80×800²/294,6×10³ = 547 мм.

Принимаем шаг хомутов у опоры s₁ = 150 мм, а в пролете — s₂ = 2s₁ = 300 мм.

Отсюда 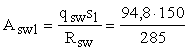= 50 мм² .

Принимаем одноветвевые хомуты диаметром 8 мм (А_sw = 50,3 мм²).

Длину участка с шагом s₁ определяем из условия обеспечения прочности согласно п. 3.24.

При этом 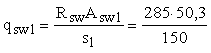= 95,6 Н/мм; q_sw2 = 0,5 q_sw1 = 47,8 Н/мм; q_sw1- q_sw2 = q_sw2 = 47,8 Н/мм.

Зададим длину участка с шагом хомутов s₁ = 150 мм равной расстоянию от опоры до второго груза l₁ = 2,8 м и проверим условие (71) при значении с, равном расстоянию от опоры до третьего груза: с = 4,3 м >l₁.

Значение c₀₁ определим по формуле (77) при q_sw = q_sw1 = 95,6 кН/м:

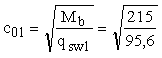= 1,5 м < 2h₀ = 1,6 м .

Так как с₀₁ = 1,5 м = с - l₁ = 4,3 - 2,8 = 1,5 м, выражение q_swc₀ заменим выражением q_sw2 (c - l₁) = 47,6 × 1,5 = 71,4 кН.

Q_b = М_b/с = 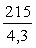= 50 кН < Q_b,min = 80,64 кН.

Принимаем Q_b = Q_b,min = 80,64 кН.

Соответствующая поперечная сила равна Q₃ = 121,8 кН (см. черт. 22, a).

Q_b + q_swc₀ = 80,64 + 71,4 = 152,04 кН > Q₃ = 121,8 кН,

т. е. прочность наклонного сечения обеспечена.

Таким образом, длину участка с шагом хомутов s₁ = 150 мм принимаем равной l₁ = 2,8 м.

Пример 14. Дано: плита перекрытия с растянутой гранью, наклонной к горизонтали, с размерами по черт. 23; бетон тяжелый класса В40 (R_bt = 1,25 МПа с учетом g_b2 = 0,9); хомуты вертикальные класса А-III, диаметром 8 мм (R_sw = 285 МПа, A_sw = 50,3 мм²) и шагом s = 100 мм; усилие предварительного обжатия Р = 980 кН; временная эквивалентная нагрузка n = 24,2 кН/м; постоянная нагрузка g = 7,8 кН/м; поперечная сила на опоре 186 кН.

Требуется проверить прочность наклонного сечения по поперечной силе.

Черт. 23. К примеру расчета 14

Р а с ч е т ведем согласно п. 3.27.

Из черт. 23 имеем h₀₃ = 300 — 75 = 225 мм. Размер b принимаем на уровне середины высоты опорного сечения:

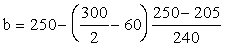= 233 мм.

Определим для опорного сечения величины j_fs, j_ns и M_bs по формулам (74), (75), (73):

b'_f - b = 3h¢_f = 3 • 60 = 180 мм;

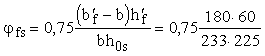= 0,154 ;

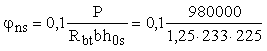= 1,495 > 0,5 .

Принимаем 1 + j_fs + j_ns = 1,5 ; j_b2 = 2 (см. табл. 29);

M_bs = j_b2 (1 + j_fs + j_ns) R_bt b h₀² = 2 × 1,5 × 1,25 × 233 × 225² = 44,2 • 10⁶ H×мм.

Определим величины q_sw и q_inc, принимая tgb = tgb₁ = 0,0815:

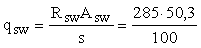= 143,3 Н/мм ;

q_inc = j_b2 (1 + j_fs + j_ns) R_bt b tg²b = 2× 1,5 × 1,25 × 233 × 0,0815² = 5,8 Н/мм;

q₁ = g + n/2 = 7,8 + 24,2/2 = 19,9 кН/м (Н/мм).

Проверим условие (87):

0,56 q_sw- 2,5 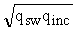= 0,56 × 143,3 - 2,5 =
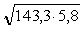= 21,1 Н/мм > q₁ = 19,9 Н/мм.

Условие (87) выполняется, и, следовательно, невыгоднейшее значение с определяем по формуле (88) :

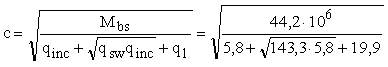= 901 мм.

Рабочая высота поперечного сечения на расстоянии с = 901 мм от опоры равна:

h₀ = h_0s + ctgb = 225 + 901 × 0,0815 = 298мм,

а ширина ребра на уровне середины высоты h = 298+75 = 373 мм равна

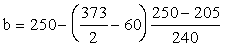= 226 мм.

Поскольку 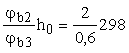= 993 мм > с = 901 мм, оставляем с = 901 мм.

Определим соответствующее значение М_b, принимая 1+j_fs+j_ns = 1,5:

М_b = 2 × 1,5 × 1,25 × 226 × 298² = 75,2 × 10⁶ H × мм.

Значение c₀ равно:

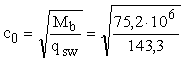= 725 мм > 2h₀ = 2 × 298 = 596 мм.

Принимаем с₀ = 596 мм.

Проверяем условие (71), принимая поперечную силу в конце наклонного сечения равной Q = Q_max- q₁c = 186 — 19,9 × 0,901 = 168,1 кН:

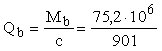= 83,5 × 10³Н ;

Q_b + q_swc₀ = 83,5 + 143,3