|
4.5. Расчетную длину элементов 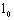 следует определять умножением их свободной длины следует определять умножением их свободной длины 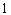 на коэффициент на коэффициент 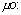
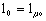 (10) (10)
согласно пп.4.21 и 6.25.
4.6. Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (5) и (6), при этом 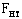 и и 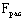 определять как суммарные площади всех ветвей. Гибкость составных элементов определять как суммарные площади всех ветвей. Гибкость составных элементов 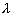 следует определять с учетом податливости соединений по формуле следует определять с учетом податливости соединений по формуле
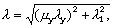 (11) (11)
|
где
|
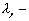
|
гибкость всего элемента относительно оси 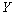 (рис.2), вычисленная по расчетной длине (рис.2), вычисленная по расчетной длине 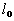 без учета податливости; без учета податливости;
| |
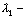
|
гибкость отдельной ветви относительно оси I - I (см.рис.2), вычисленная по расчетной длине ветви 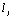 ; при ; при 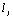 меньше семи толщин ( меньше семи толщин (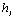 ) ветви принимают ) ветви принимают 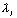 =0; =0;
| |
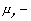
|
коэффициент приведения гибкости, определяемый по формуле
|
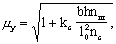 (12) (12)
|
где
|
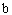 и и 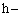
|
ширина и высота поперечного сечения элемента, см;
| |
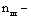
|
расчетное количество швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рис.2,а - 4 шва, на рис.2,б - 5 швов);
| |
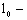
|
расчетная длина элемента, м;
| |
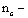
|
расчетное количество срезов связей в одном шве на 1 м элемента (при нескольких швах с различным количеством срезов следует принимать среднее для всех швов количество срезов);
| |
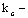
|
коэффициент податливости соединений, который следует определять по формулам табл.12.
|
При определении 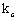 диаметр гвоздей следует принимать не более 0,1 толщины соединяемых элементов. Если размер защемленных концов гвоздей менее 4 диаметр гвоздей следует принимать не более 0,1 толщины соединяемых элементов. Если размер защемленных концов гвоздей менее 4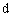 , то срезы в примыкающих к ним швах в расчете не учитывают. Значение , то срезы в примыкающих к ним швах в расчете не учитывают. Значение 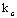 соединений на стальных цилиндрических нагелях следует определять по толщине соединений на стальных цилиндрических нагелях следует определять по толщине  более тонкого из соединяемых элементов. более тонкого из соединяемых элементов.
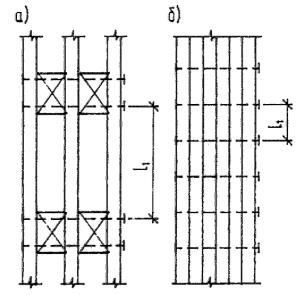
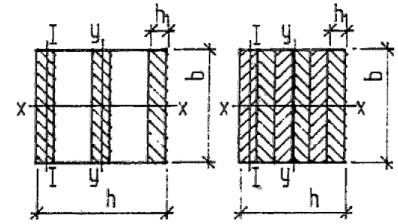
Рис. 2. Составные элементы
а - с прокладками; б - без прокладок
Таблица 12
|
Вид соединений
|
Коэффициент 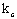 при при
| |
|
центральном сжатии
|
сжатии с изгибом
| |
|
|
| |
1. Гвозди
|
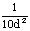
|
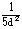
| |
2. Стальные цилиндрические нагели:
|
|
| |
а) диаметром 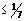 толщины соединяемых элементов толщины соединяемых элементов
|
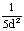
|
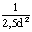
| |
б) диаметром >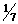 толщины соединяемых элементов толщины соединяемых элементов
|
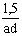
|
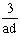
| |
3. Дубовые цилиндрические нагели
|
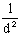
|
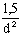
| |
4. Дубовые пластинчатые нагели
|
-
|
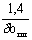
| |
5. Клей
|
0
|
0
| |
Примечание: Диаметры гвоздей и нагелей 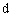 , толщину элементов , толщину элементов 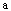 , ширину , ширину 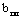 и толщину и толщину 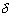 пластинчатых нагелей следует принимать в см. пластинчатых нагелей следует принимать в см.
|
При определении 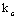 диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов. диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов.
Связи в швах следует расставлять равномерно по длине элемента. В шарнирно-опертых прямолинейных элементах допускается в средних четвертях длины ставить связи в половинном количестве, вводя в расчет по формуле (12) величину 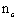 , принятую для крайних четвертей длины элемента. , принятую для крайних четвертей длины элемента.
Гибкость составного элемента, вычисленного по формуле (11), следует принимать не более гибкости 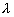 отдельных ветвей, определяемой по формуле отдельных ветвей, определяемой по формуле
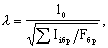 (13) (13)
|
где
|
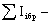
|
сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных оси 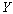 (см.рис.2); (см.рис.2);
| |
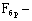
|
площадь сечения брутто элемента;
| |
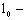
|
расчетная длина элемента.
|
Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось 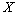 на рис.2), следует определить как для цельного элемента, т.е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться п.4.7. на рис.2), следует определить как для цельного элемента, т.е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться п.4.7.
Если ветви составного элемента имеют различное сечение, то расчетную гибкость 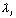 ветви в формуле (11) следует принимать равной: ветви в формуле (11) следует принимать равной:
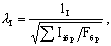 (14) (14)
определение 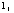 приведено на рис.2. приведено на рис.2.
4.7. Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий:
а) площади поперечного сечения элемента 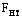 и и 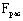 следует определять по сечению опертых ветвей; следует определять по сечению опертых ветвей;
б) гибкость элемента относительно оси 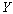 (см.рис.2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь - только опертых; (см.рис.2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь - только опертых;
в) при определении гибкости относительно оси 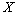 (см.рис.2) момент инерции следует определять по формуле (см.рис.2) момент инерции следует определять по формуле
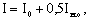 (15) (15)
|
где
|
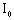 и и 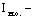
|
моменты инерции поперечных сечений соответственно опертых и неопертых ветвей.
|
4.8. Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле
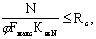 (16) (16)
|
где
|
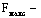
|
площадь поперечного сечения брутто с максимальными размерами;
| |
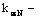
|
коэффициент, учитывающий переменность высоты сечения, определяемый по табл.1 прил.4 (для элементов постоянного сечения 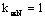 ); );
| |
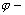
|
коэффициент продольного изгиба, определяемый по п.4.3 для гибкости, соответствующей сечению с максимальными размерами.
|
Изгибаемые элементы
4.9. Расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования (см. пп.4.14 и 4.15), на прочность по нормальным напряжениям следует производить по формуле
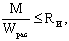 (17) (17)
|
где
|
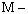
|
расчетный изгибающий момент;
| |
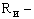
|
расчетное сопротивление изгибу;
| |
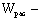
|
расчетный момент сопротивления поперечного сечения элемента. Для цельных элементов 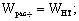 для изгибаемых составных элементов на податливых соединениях расчетный момент сопротивления следует принимать равным моменту сопротивления нетто для изгибаемых составных элементов на податливых соединениях расчетный момент сопротивления следует принимать равным моменту сопротивления нетто 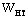 , умноженному на коэффициент , умноженному на коэффициент 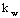 ; значения ; значения 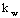 для элементов, составленных из одинаковых слоев, приведены в табл.13. При определении для элементов, составленных из одинаковых слоев, приведены в табл.13. При определении 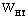 ослабления сечений, расположенные на участке элемента длиной до 200 мм, принимают совмещенными в одном сечении. ослабления сечений, расположенные на участке элемента длиной до 200 мм, принимают совмещенными в одном сечении.
|
Таблица 13
|
Обозначение коэффициентов
|
Число слоев в элементе
|
Значение коэффициентов для расчета изгибаемых составных элементов при пролетах, м
| |
|
|
2
|
4
|
6
|
9 и более
| |
|
|
|
|
|
| |
|
2
|
0,7
|
0,85
|
0,9
|
0,9
| |
|
3
|
0,6
|
0,8
|
0,85
|
0,9
| |
|
10
|
0,4
|
0,7
|
0,8
|
0,85
| |
|
2
|
0,45
|
0,65
|
0,75
|
0,8
| |
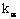
|
3
|
0,25
|
0,5
|
0,6
|
0,7
| |
|
10
|
0,07
|
0,2
|
0,3
|
0,4
| |
Примечание. Для промежуточных значений величины пролета и числа слоев коэффициенты определяются интерполяцией.
|
4.10. Расчет изгибаемых элементов на прочность по скалыванию следует выполнять по формуле
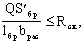 (18) (18)
|
где
|
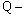
|
расчетная поперечная сила;
| |
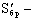
|
статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;
| |
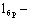
|
момент инерции брутто поперечного сечения элемента относительно нейтральной оси;
| |
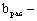
|
расчетная ширина сечения элемента;
| |
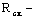
|
расчетное сопротивление скалыванию при изгибе.
|
4.11. Количество срезов 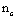 , равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию , равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию
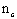 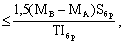 (19) (19)
|
где
|
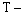
|
расчетная несущая способность связи в данном шве;
| |
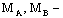
|
изгибающие моменты в начальном 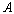 и конечном и конечном 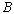 сечениях рассматриваемого участка. сечениях рассматриваемого участка.
|
Примечание. При наличии в шве связей разной несущей способности, но
одинаковых по характеру работы (например, нагелей и гвоздей), несущие
способности их следует суммировать.
4.12. Расчет элементов цельного сечения на прочность при косом изгибе следует производить по формуле
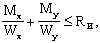 (20) (20)
|
где 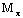 и и 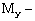
|
составляющие расчетного изгибающего момента для главных осей сечения 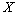 и и 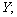
| |
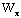 и и 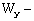
|
моменты сопротивлений поперечного сечения нетто относительно главных осей сечения 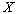 и и 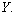
|
4.13. Клееные криволинейные элементы, изгибаемые моментом 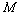 , уменьшающим их кривизну, следует проверять на радиальные растягивающие напряжения по формуле , уменьшающим их кривизну, следует проверять на радиальные растягивающие напряжения по формуле
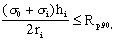 (21) (21)
|
где
|
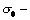
|
нормальное напряжение в крайнем волокне растянутой зоны;
| |
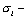
|
нормальное напряжение в промежуточном волокне сечения, для которого определяются радиальные растягивающие напряжения;
| |
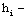
|
|
